Co je to Kalmanova filtrace?
Kalmanova filtrace je speciální matematický aparát (algoritmus) pro filtraci signálů v časové oblasti. Výhodou tohoto systému je schopnost získat čistý signál a hodnoty ze zašuměného signálu nebo jinak znehodnoceného souboru hodnot, i bez jakéhokoliv poznatku o rušení. Prakticky lze takto matematicky zjistit hodnoty, které jsou přímým měřením těžko zjistitelné, protože se při samotném aktu měření do získaných hodnot indukují chyby měřících přístrojů nebo okolní působící šum a rušení.
Ve zjednodušené podobě jde o predikční-estimační algoritmus, který z předchozích a i následných budoucích dat snaží předpovědět průběh signálu, tedy vždy z průběhu minulých vzorků signálu vzorky následující, např. neznámí čistý signál bez rušení jen z měřeného. Ty jsou pak konfrontovány s opravdu naměřenými vzorky a jejich rozdíl se opět využívá k zlepšení odhadu dalších budoucích vzorků.
K čemu to je ?
Výhoda Kalmanovy filtrace je ve dvou vlastnostech:
- proti filtračním algoritmům pracující ve frekvenčním oblasti (spektru) dokáže provést téměř stejně kvalitní filtraci v časové oblasti. Protože
v prvopočátku máme každý signál vždy v časové oblasti, odpadá často implementačně
a na výpočetní výkon náročná Fourierova transformace.
- proti jiným filtračním algoritmům pracující také v časové oblasti zde není nutné cokoliv vědět o hledaném čistém (neporušeném) signálu ani o šumu a rušení, které na něj působily. Prostě se přímo aplikuje na naměřený soubor dat nebo nahraný obrazový či zvukový signál.
Ze své praktické zkušenosti mohu potvrdit, že Kalmanova filtrace je vhodná pro:
- filtraci zarušených stacionárních signálů
- odšumění kvazistacinárních signálů
- hledání silně zarušených harmonických signálů
- odstranění bílého i barevného šumu
- zpřesnění naměřených hodnot - zlepšení přesnosti měření
- řízení a navigace robotů
- odhad budoucnosti (průběh křivky) z minulosti
- apod.
Na jakém principu Kalmanova filtrace pracuje ?
Když to vezmeme od samotného jádra a co nejjednodušeji, lze celý Kalmanův algoritmus popsat jako průměrování odchylek naměřených hodnot od odhadovaných hodnot a jejich nejistot, tedy pravděpodobností, že je naměřená hodnota je správná. Například si lze představit jachtu plující po moři a my se snažíme určit její přesnou polohu a směr plavby. V určitých měřících okamžicích zjišťujeme její okamžité polohy s nějakou chybou (přesností). Kalmanův algoritmus je pak schopen hodnoty zpřesnit tak, že určuje rozdíly odhadnuté (predikované) polohy a provádí průměrování těchto chybových hodnot se zapomínáním starších vzorků. Na základě průběhu předchozích chyb, resp. jejich rozptylu, dochází k odhadu nejbližších následujících poloh.
Celý Kalmanův algoritmus tak běží v jakém si kruhu:
- odhad hledané veličiny a predikce nového stavu z předchozích
- korekce predikce započtením nové reálné naměřené hodnoty
Celý výpočetní algoritmus je složen z několika rovnic, které vycházejí z předpokladu, že analyzovaný signál (posloupnost hodnot) byl generován tzv. autoregresním modelem (AR modelem) buzený určitým řídícím/budícím šumem w(n). V praxi samozřejmě to tak být nemusí, ale Kalmanův algoritmus tak pracuje. Vychází se zde z toho, že většinu signálů lze takto uspokojivě popsat.
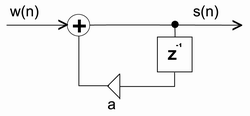
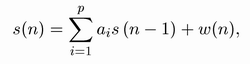
Obr. 1. Blokové schéma základního AR modelu pro generování čistého signálu a jeho matematický popis
s (n)... stavová veličina = čistý signál
w (n)... řídící/budící veličina = budící signál (např. u řeči bílý šum s impulsy)
ai ... koeficienty AR modelu
z ... zpoždění
V aplikacích měřicí techniky představuje s(n) přímým měřením těžko zjistitelnou hodnotu měřené veličiny, protože při samotném aktu měření se do získaných hodnot indukuje jak chyba měřících přístrojů, tak i okolní působící šum a rušení. V těchto aplikacích se právě hodí použít Kalmanovu filtraci, která dokáže predikovat hledaný neznámý signál i šumy, které jsou v naměřeném signálu obsaženy.
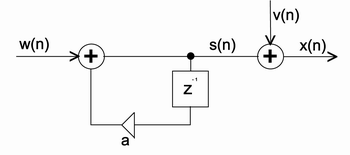
Obr. 2. Blokové schéma generujícího AR modelu doplněného o rušení v(n) působící během měření / snímání
w(n), v(n) ... nekorelované diskrétní bílé šumy s kovariančními maticemi Q a R
Obecně lze algoritmus Kalmanovy filtrace popsat blokovým schématem na obrázku 3. a výpočet rozdělit do následujících kroků:
- Naměřená hodnota x je porovnávána s hodnotou odhadnutou (predikovanou)
- Zjištěný rozdíl (chyba) je vynásoben konstantou K (tzv. Kalmanův zisk), která je průběžně počítána na základě předchozích zjištěných chyb.
- Následně probíhá korekce předchozí odhadnuté (predikované) čisté hodnoty s hledané veličiny .
- Dále dochází k predikci nové hodnoty s násobením minulých predikovaných hodnot koeficienty matice A.
- Odhad "špinavé" zarušené hodnoty x z výstupní veličiny pro porovnání s novou naměřenou hodnotou.
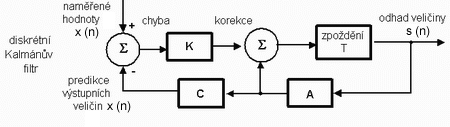
Obr. 3. Obecné a základní blokové schéma Kalmanovy filtrace
Kalmanova filtrace s odhadem parametrů pomocí NLMS
Ve výše uvedeném obecném blokovém schématu na obrázku 3. se objevují koeficienty, resp. v případě většího řádu než 1 jde o matice koeficientů, které je potřeba nějak určit. Existuje mnoho metod jejich určení, ale pokud má být algoritmus schopný odšumovat i "nekonečný" nestacionární signál, musí být i určení těchto koeficientů realizováno jejich průběžným výpočtem v závislosti na intenzitě a barvě šumu. Jednou z možností je LMS nebo NLMS algoritmus, který dle mých zkoušek a zkušenosti dobře funguje i pro kvazistacionární signály, například řeč. Blokové schéma celkového systému Kalmanovy filtrace s NLMS prvního řádu je na obrázku 4.
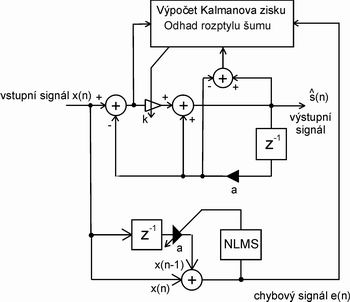
Obr. 4. Blokové schéma Kalmanovy filtrace s NLMS pro výpočet koeficientů AR modelu
NLMS část provádí odhad koeficientů a, což jsou vlastně odhadované koeficienty AR modelu čisté řeči, který by hledaný signál vytvořil, i získání chybového dekorelovaného chybového signálu e(n), představující úroveň bílého šumu obsaženého ve celé směsi měřeného signálu. To je jak budící bílý šum AR modulu hledaného signálu, tak přidaný bílý šum vzniklý šumem měřících a snímacích prvků či rušením okolím. Pro tyto účely se NLMS algoritmus hodí lépe než LMS, protože poskytuje rychlejší výsledky, resp. rychleji konverguje.
Je logické, že pokud je šum místo bílého barevný, tzn. bílý šum modelovaný dalším AR modelem, jsou jeho parametry automaticky zahrnuty i do koeficientů. Vzniká zde sice chyba, která se však kompenzuje "regulací" koeficientu k (Kalmanův zisk) z průběhu předchozích několika odchylek (korekcí) reálného a predikovaného signálu. Tato metoda se nazývá měření diferencí a umožňuje jednoduše Kalmanovu filtraci nasadit i pro filtraci například mikrofonem snímané řeči zasažené hlukem jedoucího automobilu.
Samotná Kalmanova filtrace se provádí následujícími 4 rovnicemi, které jsou pro jednoduchost vyjádřeny 1. řádu, podobně jako blokové schéma na obrázku 4. V případě vyšších řádů je nutné místo jednoduchých koeficientů dosadit matice koeficientů a místo hodnot signálů dosadit vektory vzorků. Tak například pro 2.řád by koeficienty reprezentovaly matice 2x2 a signály vektory se příslušnými zpožděnými vzorky (n-1) a (n-2). Složitému maticovému počítání, které není u reálných implementací jednoduché naprogramovat, se dá za určitých podmínek vyhnout rozdělením měřeného signálu do několika pásem pomocí banky filtrů a místo přímého nasazení maticové verze tak použít Kalmanovu filtraci 1. řádu zvlášť v každém pásmu banky filtrů. Výpočetní náročnost i naprogramování je výrazně jednodušší. Mě se pro filtraci řeči s dobrými výsledky osvědčilo rozdělení zarušeného řečového signálu do 4 pásem.
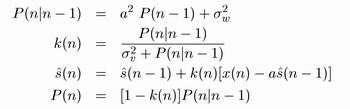
Rov. 1. Základní rovnice realizující samotnou Kalmanovu filtraci 1. řádu
Jednotlivé rovnice provádějí následující úkony:
- První rovnice provádí predikci chybové hodnoty (v maticovém zápise kovarianční matice), tj. odhad jaký bude rozdíl nové naměřené zarušené hodnoty proti hledané čisté.
- Druhá rovnice provádí z této chybové hodnoty a z hodnoty rozptylu rušícího šumu výpočet (predikci) nové hodnoty Kalmanova zisku.
- Třetí rovnice je prakticky ta hlavní, protože provádí korekci předchozího
odhadnutého vzorku čistého signálu o rozdíl proti skutečnému naměřenému vzorku.
V této variantě Kalmonovy filtrace, kde proti blokovému schématu na obrázku 3. je hodnota C=1, je prakticky nová predikovaná hodnota zahrnuta uvnitř této rovnice (člen a.s(n-1)).
- Poslední rovnice provádí určení (estimaci) chybové hodnoty v závislosti na její dříve odhadnuté hodnotě a nové hodnotě Kalmanova zisku.
Prakticky se pořád točíme v kruhu těchto 4 rovnic, kde všechny rovnice před 3. rovnicí predikují nové hodnoty a následující rovnice již korigují své hodnoty podle nově změřeného vzorku. Proti blokovému schématu na obrázku 3. zde přímo nevyužíváme predikované hodnoty našeho hledaného signálu s(n), ale až korigované hodnoty dle reálného změřeného vzorku. Výsledná hodnota je přesnější a přeci nepotřebujeme predikovat, ale filtrovat. Výhodou této vnitřní predikce je vlastnost, že bez zpoždění máme okamžitě po změření vzorku "špinavého signálu" vyfiltrovaný vzorek čistý.
Pro výpočet koeficientů autoregresního modelu (AR modelu) se využívá již zmíněného NLMS algoritmu. Využít lze klasické následující vzorce, kde e(n) je dekorelovaný signál (v ideálním případě bílý šum) a a(n) je nový koeficient:
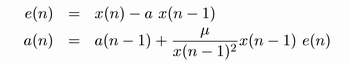
Rov. 2. Rovnice algoritmu NLMS pro výpočet koeficientů AR modelu
Pro výše uvedené rovnice je však nutné zjistit neznámé hodnoty rozptylu σw bílého budícího šumu w(n) AR modulu čistého signálu a rozptylu σv rušivého šumu v(n), který odstraňujeme. Odhad rozptylu σw lze zjistit pomocí již zmíněné metody měření diferencí, dle následujících rovnic:
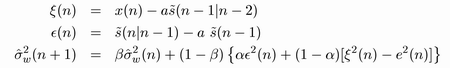
Rov. 3. Rovnice pro odhad rozptylu budícího šumu AR modulu čistého signálu - metoda "Měření diferencí"
Konstanty α a β slouží jako průměrovací váhy. Konkrétně α se používá při vzájemném průměrování rozptylů signálu ε (n) a rozdílů signálů ζ (n) a e (n). Konstanta β slouží pro updatování rozptylu z předchozích hodnot. Jako hodnotu rozptylu σv lze použít rozptyl chybového signálu e(n) získaného z výstupu NMLS algoritmu.
TEST Kalmanovy filtrace - příklady výsledků z odšumování
Zašuměný sinusový signál
Prvním příkladem práce algoritmu Kalmanova filtrace je odšumění směsi sinusového signálu a bílého šumu pro různá řády filtrace. Jak je vidět z obrázků 5. až 7., neplatí zde úměra, že čím větší řád, tím lepší výsledky. Zde asi nejlepší filtraci provádí struktura 2. řádu, i když výsledek struktury 1. řádu je skoro stejně dobrý, pouze zde má sinusovka nižší amplitudu. Výsledek struktury 3. řádu již moc sleduje šum a málo "vyhlazuje".
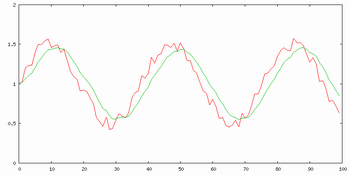
Obr. 5. Průběh Kalmanovy filtrace 1. řádu (zelený průběh) pro bílým šumem poničenou sinusovku (červený průběh)
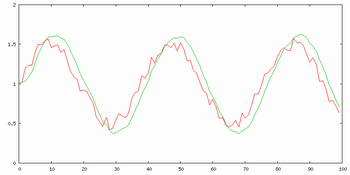
Obr. 6. Průběh Kalmanovy filtrace 2. řádu (zelený průběh) pro bílým šumem poničenou sinusovku (červený průběh)
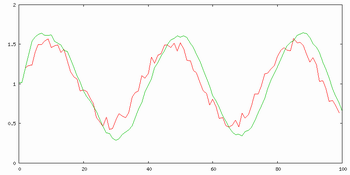
Obr. 7. Průběh Kalmanovy filtrace 3. řádu
Filtrace řeči Kalmanovou filtreací s NLMS
Osobně jsem testoval Kalmanovu filtraci s NLMS algoritmem pro aplikaci odšumování řeči na PC v programu Matlab a na signálovém procesoru firmy TEXAS Instruments TMS32VC5416. K testování jsem použil české věty "Zítra snad nebude pršet" a "Redakci, prosím.", které jsem smíchal s umělým bílým šumem vygenerovaným v programu Matlab a s reálným hlukem jedoucího linkového autobusu Karosa v různých intenzitách, tj. s různým poměrem řeči a šumu v decibelech.
Na obrázku 8. je příklad výsledku z PC z programu Matlab pro směs věty "Zítra snad nebude pršet" (horní modrý průběh) a bílého šumu s odstupem 0 dB (směs = dolní modrý průběh). Tento signál byl vpuštěn na vstup programu realizující Kalmanovu filtraci s NLMS 1. řádu umístěnou ve čtyřech pásmech banky filtrů. Výsledný odšuměný signál (dolní zelený průběh) je prakticky téměř bez slyšitelného šumu a vcelku dobře srozumitelný běžným poslechem. Číselně došlo k odšumění o cca 8 dB.
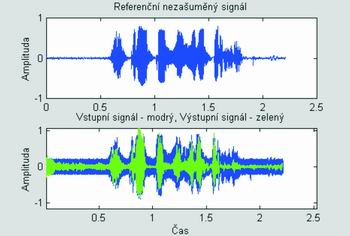
Obr. 8. Odšumění věty "Zítra snad nebude pršet" od bílého šumu na PC v programu Matlab
Na obrázku 9. je pak stejná řeč stejně zašuměná, ale výsledný signál (červený průběh) je dosažen reálnou filtrací DSP TI TMS32VC5416. Zarušený signál byl na vstup DSP přiváděn jako analogový přes A/D převodník Burr-Brown a po filtraci opět převeden D/A převodníkem Burr-Brown na analogový signál. Algoritmus jsem naprogramoval v jazyku C s některými částmi přímo v ASM (asembleru), abych dosáhl lepší optimalizace programu algoritmu a rychlejšího zpracování. Výsledkem byl prakticky poslechově úplně odstraněný šum, přičemž však došlo na některých místech i k slabému zkreslení průběhu požadované řeči. Řeč je přesto dobře srozumitelná. V číselném vyjádření došlo o odšumění o 7.5 dB.
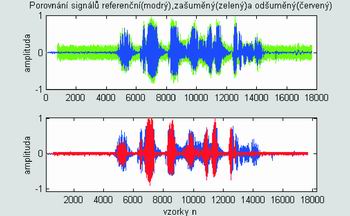
Obr. 9. Odšumění věty "Zítra snad nebude pršet" od bílého šumu realizovaném na DSP TI TMS32VC5416
Konečně na obrázku 10. je věta "Redakci, prosím" zašuměná barevným šumem (hlukem) jedoucího autobusu Karosa v poměru 0 dB. Jak je patrné z vyfiltrovaného červeného signálu, algoritmus si poradil i s tímto případem dost dobře, pouze v signále zůstala složka impulsního hluku auta projíždějícího v protisměru, který se do hluku autobusu "vpašoval" přes otevřené okno. Toto krátké, téměř impulsní rušení algoritmus omylem považoval za řeč. Odšuměná řeč je však dobře srozumitelná a zbylý hluk při poslechu jen velmi slabý. Číselně došlo ke zvýraznění řeči o cca 6 dB.
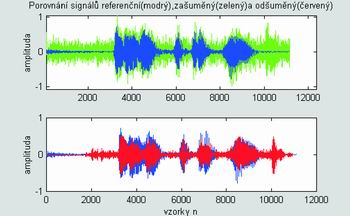
Obr. 10. Odšumění věty "Redakci, prosím" od šumu jedoucího automobilu realizovaném na DSP TI TMS32VC5416
Závěr
Kalmanova filtrace je účinný, ale dost složitý algoritmus, zvlástě pro řády vyšší než 1. V tomto článku jsem se pokusil nějak nenáročně alespoň nastínit jeho princip a uvést některé výsledky, které lze implementací algoritmu dosáhnout. Zatímco v případě filtrace vyšších řádů je nutné provádět dost programově náročná maticová násobení, v případě rozdělení signálu bankou filtrů do frekvenčně užších pásem lze použít již jen Kalmanovu filtraci 1. řádu a maticové výpočty se tak smrsknou na obyčejné skalární násobení. To již není problém snadno realizovat i na obyčejném DSP - viz filtrace řeči na obrázkách 9. a 10.
Antonín Vojáček
vojacek@ hwg.cz
DOWNLOAD & Odkazy
- Praktické informace o použití Kalmanovy filtrace v měřící technice - Kalmanur.doc, http://measure.feld.cvut.cz/groups/edu/vmd/Kalmankor.htm
- informace k Wienerovu a Kalmanovu filtru - http://radio.feld.cvut.cz
- Petr Šimeček: "Časové řady II - Filtrace", http://atrey.karlin.mff.cuni.cz/~simecek/princip/slidy5.pdf
- Michal Kutil, Tomáš Cigánek: "Kalmanův filtr", http://www.tim.cz/skola/archiv/mtr/uloha5.pdf
- pěkný článek o filtraci dat - http://robotika.cz/guide/filtering/en