Co je to korelace?
Korelace je algoritmus umožňující jednoduše vzájemně porovnávat dva digitalizované signály (posloupnosti vzorků). Výsledkem porovnání je opět posloupnost čísel vyjadřující podobnost dvou porovnávaných signálů a některé původně skryté vlastnosti signálů. Takto lze například zjišťovat periodicitu a periodu neznámého signálu, nalézt neznámou hodnotu zpoždění dvou stejných nebo podobných signálů, nebo objevit konkrétní hledaný signál skrytý v silném rušení (šumu).
Algoritmus je založen na vzájemném násobení vzorků signálu, z nichž se následně provádí součet (suma). Tím, že se využívá jen operací násobení a sčítání, je algoritmus vhodný pro implementaci i na malých signálových procesorech, MCU nebo FPGA.
K čemu to je ?
Algoritmus korelace se téměř vždy využívá v aplikacích, kde se nějaký signál vysílá za účelem detekce a opět přijímá jeho odražená verze nebo složka, např. radary, světelné závory, indukční a ultrazvukové senzory pro detekci objektů a jejich přiblížení. V těchto případech totiž spolu s užitečným odraženým signálem dopadá na snímač/přijímač senzoru i rušení a od okolních podobných senzorů nebo jiných zařízení.
Typickým a snadno představitelným příkladem je optická závora, která pro detekci vždy vysílá skupinu rychle po sobě jdoucích impulsů, které v případě odrazu od objektu nebo odrazky dopadají zpět na přijímač, který je převádí opět na elektrický signál. Ale spolu s tímto signálem mohou na přijímač náhodně dopadat různé světelné záblesky z okolních optických senzorů nebo zdrojů světla. Aplikací algoritmu korelace, který běží v mikroprocesoru a porovnává vysílaný elektrický signál s přijímaným, lze vyloučit uvedené náhodné impulsy, které by jinak mohly způsobit falešnou detekci objektu.
Výpočet korelace a autokorelace
Pro výpočet korelace digitalizovaných signálů existuje jednoduchý vzorec pro výpočet:
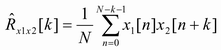
Vzorec 1. Vztah pro korelaci dvou signálů X1 a X2
Konkrétně je jde o vzorec pro tzv. vychýlený odhad korelace dvou signálů X1 a X2. Celý výpočet se slovně dá popsat jako součet (suma) součinů jednoho signálu (zde X1), který lze také označit jako referenční porovnávací, s druhým signálem (X2) - porovnávaným. Celá suma je pak dělena počtem vzorků porovnávaných signálů. Prakticky jde o to, že konkrétní k-tá hodnota korelace se provádí násobím referenčního signálu s tím druhým neznámým, který je vůči němu posunut o počet vzorků k.
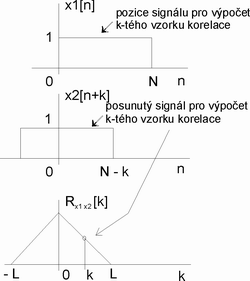
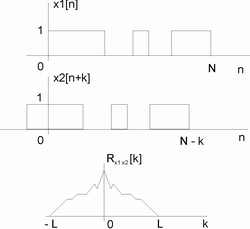
Obr. 1. Graficky vyjádřený výpočet k-tého vzorku korelace
Na obrázku 1. je to vysvětleno graficky. K výpočtu vyznačeného k-tého vzorku posloupnosti, resp. grafu, korelace R je nutné vzájemně pronásobit vzorky vyznačeného obdélníkového signálu X1 s posunutým obdélníkovým signálem X2. Například pro 4. koeficient korelace (k=4) jsou signály X1 a X2 vzájemně posunuty o 4 vzorky (k=4) - viz obrázek 1. Výsledkem je tedy korelace R = posloupnost nebo graf hodnot (koeficientů) ukazujících, jak jsou oba signály podobné, jestliže je vůči sobě posouváme. Průběh grafu tzv. vychýleného odhadu korelace má vždy tvar podobný trojúhelníku, i když v případě složitějších signálů je to jen jeho silueta (viz dále). Maximální hodnota korelace vždy odpovídá momentu, kdy jsou signály vzájemně nejvíc podobné. Pozice vrcholu, tedy jemu odpovídající hodnota k, pak určuje vzájemné posunutí obou porovnávaných signálů - viz obrázek 2. Na něm je obdélníkový signál X2 posunut například vlivem zpoždění průchod signálu přenosovou cestou o hodnotu "zpoždění", které může nabývat např. hodnoty 5 vzorků (časová hodnota zpoždění je pak dána vynásoběním velikostí vzorkovací periody). Vrchol grafu korelace pak nastává právě pro hodnotu k=zpoždění. V našem modelovém případě by tedy maximální hodnota korelace nastala pro k=5.

Obr. 2. Zjištění neznámé hodnoty zpoždění mezi signály pomocí korelace
Největší hodnota korelace (vrchol v grafu) určuje velikost vzájemného posunutí obou signálů, aby byly vzájemně co nejvíce podobné. Díky tomu lze nalézt podobnost i dvou stejných signálů, které jsou například vlivem zpoždění šířením vzájemně časově posunuty.
Speciální případ je pak tzv. autokorelace, kdy se porovnávají dva shodné signály, tzn. X1 = X2. Pak se vzorec zjednoduší na:
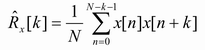
Vzorec 2. Vztah pro autokorelaci
Zatímco v korelaci použijeme hlavně v případech, kdy chceme zjistit, zda druhý signál se podobný nebo shodný s tím prvním-referenčním, autokorelace se používá pro získání parametrů a vlastností neznámého signálu X[n] nebo k zjištění hodnot posloupnosti (průběh grafu) korelace v ideálním případě, kdy by byly oba signály X1 a X2 shodné. U autokorelace vždy platí, že její maximální hodnota vždy odpovídá nulovému koeficientu (R[0]), tzn. nulovému zpoždění.
Další příklady průběhů korelace
Mezi další použití korelace nebo častěji autokorelace je zjišťování periody, resp. frekvence, neznámého periodického signálu. Výhodou použití korelace od jiných metod je schopnost zjišťovat velikost periody různých signálů, ať již neharmonických, tak i signálů různě skládaných a složitých, kde délka periody není ani z časového průběhu a frekvenčního spektra signálu na první pohled zřetelná.
Na obrázku 3. je jednoduchý příklad grafu korelace dvou stejných trojúhelníkových signálů s periodou 4 vzorky. Výsledkem je graf s klasickým maximem v místě k=0 (signály nejsou vzájemně posunuté) a siluetou připomínající tvar trojúhelníku. Lze v něm však mimo hlavní vrchol nalézt i menší, který se vytvořil díky nalezené periodicitě, opakování stejného tvaru vícekrát v signálu délky N. Vzdálenost menšího vrcholu od hlavního je právě 4 vzorky, tedy hodnota periody signálu.
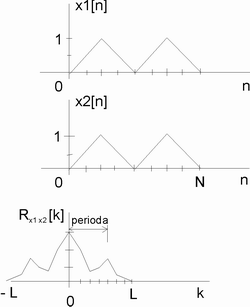
Obr. 3. Příklad grafu korelace periodického signálu
Na obrázku 3. jde jen o co nejvíce zjednodušenou verzi pro co nejjednodušší demonstraci. V praxi však je vhodné počítat korelaci (autokorelaci) za účelem zjištění periody z většího počtu period počítaného signálu, tzn. z většího počtu vzorků. Ve výsledném grafu se pak objeví více menších špiček, které budou též od sebe vzdáleny o hodnotu periody. Tím se lze vyhnout možnému falešnému detekování periody úplně neznámého signálu, který periodický třeba vůbec není.
Příkladem může být obrázek 4., kde je spočítán graf korelace (vlastně autokorelace - signály X1 a X2 jsou stejné) z neperiodického obdélníkového signálu složitějšího průběhu. V grafu korelace se také nacházejí mimo hlavní špičky (vrcholu) poblíž i malá další špička. Ta ovšem neznamená nic konkrétního a jde jen o jev vzniklý díky vzdálené podobnosti jednotlivých obdélníků v posloupnosti signálu.
Obr. 4. Průběh korelace složitějšího průběhu signálu
Implementace
Implementace samotného algoritmu je v celku jednoduchá. Stačí k tomu obecně použít jen operace násobení a sčítání. V případě programovacího jazyka by kód realizující vzorec 1. mohl vypadat například následovně:

Obr. 5. Příklad naprogramovaní vzorce pro korelaci v jazyku C
Závěr
Algoritmus korelace patří mezi základní algoritmy číslicového zpracování signálů, bez kterého by nefungovaly dnešní vyspělé detekční systémy, zařízení a programy zpracovávající hlas, řeč, obraz, filmy nebo fotky. Často však korelace bývá součástí rozsáhlejšího systému nebo je zakomponován ve složitějším algoritmu. Protože tento článek byl pojat a napsán pro co nejširší okruh čtenářů, jsou zde co nejjednodušeji uvedeny jen základní informace a popis. Proto se všem odborníkům a matematikům omlouvám za nepřesnosti, které vznikly právě co největším zjednodušením problému. Pro podrobnější informace o korelaci i dalších algoritmech číslicového zpracování signálu.
Antonín Vojáček
vojacek@ hwg.cz
DOWNLOAD & Odkazy
- Doporučuji pro všechny zájemce o problematiku číslicového zpracování signálů: Jan Jiří, "Číslicová filtrace, analýza a restaurace signálů", nakladatelství BEN, 2004, 427 stran - lze koupit na www.ben.cz




