Co je to adaptivní filtr ť
Adaptivní filtr je způsob, jak filtrovat parazitní rušení ze signálu užitečného (signál ze senzoru, hudba, řeč apod.), jestliže s časem mění svoje parametry nebo konkrétně dopředu jeho parametry neznáme. V druhém případě může být rušení časové stabilní, ale dopředu nic o něm nevíme. V tomto případě pak nelze navrhnout potřebný pevný filtr. Typický problém je silná rušení síťovým kmitočtem, který navíc nemusí mít po celý čas přesně pevnou frekvenci, nebo se například objevuje a mizí.
Jako adaptivní filtr se využívá známý FIR filtr, jehož koeficienty jsou průběžně přenastavovány nějakým algoritmem. Ten monitoruje vstupní a výstupní signál z filtru a z chybového signálu se snaží co nejoptimálněji nastavit koeficienty filtru tak, aby chyba byla co nejmenší.
K čemu to je ť
Jednoduchý adaptivní filtr tvořený filtrem FIR a obvykle nějakým algoritmem na bázi algoritmu LMS (popis dále) se nejvíce hodí na dvě aplikace:
- Odstranění neznámého harmonického časově málo proměnného signálu z užitečného žádaného signálu
- Odstranění širokopásmového náhodného šumu (blízký bílému) z užitečného signálu s pomalými změnami v porovnání se šumem
Jak je vidět jde přesně o dvě protikladné funkce. Důležité je, aby se oba signály, které mají být správně rozlišeny, měli rozdílné rychlosti změn (periodu).
Z obecného praktického použití lze jmenovat:
- Odstranění sinusových rušících signálů na indukovaných ve vedení od senzoru
- Automatické zjištění a dorovnání útlumu některých frekvencí způsobené vedením
- Odstranění síťového rušení 50Hz z přenášeného signálu
- Odstranění šumu a rušení ze zvuku
- Parametrizace řeči - metoda LPC koeficientů
Na jakém principu to pracuje ť
Pro teoretickou i praktickou ukázku jsem si vybral adaptivní FIR filtr, jehož koeficienty jsou řízeny tzv. LMS algoritmem. Následně ho používám jako prediktor nebo estimátor pro odstranění několika rušících sinusových signálů.
Při popisu principu lze vyjít z adaptivního systému ALE, který funguje na principu vyhledávání rušících harmonických signálů pomocí korelace vstupního signálu se týmž signálem, ale časově (vzorkově) posunutém. Zde se využívá situace, že neharmonický proměnný signál má přes delší časový úsek autokorelaci blížící se autokorelaci šumu narozdíl od autokorelace dlouhodobě stacionárního (neměnného) harmonického signálu, která vykazuje periodicitu a její hodnoty pomalu klesají. Tímto způsobem lze vhodným vzájemným posunutím signálu vybrat rušící harmonický signál.
Adaptivní filtr FIR (viz. obrázek 1.), jehož koeficienty jsou řízeny LMS algoritmem lze popsat následující rovnicí:
y [n] = d [n] - s [n] = d[n] - ( b1 [n-1] * d [n-D] + b2 [n-1] * d [n-(D+1)] + .. + bM [n-1] * d [n-(D+M)] ,
kde y [n] je výstup z filtru, b [n-1] jsou jednotlivé koeficienty filtru vypočítané v předchozím kroku a d [n] je vstupní signál, resp. jeho zpožděné vzorky, například d [n-D] - vstupní signál zpožděný o D vzorků.
Koeficienty jsou obvykle řízeny tzv. LMS algoritmem (Least Mean Square algorithm), případně je modifikacemi (NLMS apod.). Zde použitý LMS algoritmus lze naprogramovat (realizovat vztahem):
bP [n] = bP [n-1] + mi * d [n] *e [n] ,
kde za P se dosadí číslo příslušného koeficientu, mi je tzv. konstanta zapomínání a e [n] je chybový signál, který v případě na obrázku 1. odpovídá výstupu. Tzn. e [n] = y [n].
Volba velikosti filtru, tzn. řád filtru M lze obecně správně volit podle vzorce:
M = 2 × počet rušících sinusovek
Ale takto realizovaný filtr FIR bude mít propustné pásmo pro výběr sinusovky dost široké a z užitečného signálu vybere (potlačí) i užitečné složky spektra signálu. Navíc často nevíme kolik rušících signálu se v budoucnu v nainstalovaném systému bude vyskytovat. To lze řešit dvěma způsoby, které ve výsledku vedou přibližně k stejnému cíly:
- STRUKTURA 1 : adaptivní FIR filtr typu estimátor s vysokým řádem M - viz. obrázek 1.
- STRUKTURA 2: adaptivní FIR filtr typu estimátor (viz. obrázku 1) s nízkým řádem M + prediktor ( přísnější filtr s užším propustným pásmem) - viz. obrázek 2.
STRUKTURA 1 - adaptivní filtr typu estimátor s řádem M1= 50
Jde tedy přímo o strukturu popsanou podorobně výše. řád byl zvolen náhodně a však mnohokrát větší než počet rušících sinusových signálů (v mém případě 3).

Obr. 1. Blokové schéma adaptivního filtru FIR typu estimátor
STRUKTURA 2 - adaptivní filtr složený z estimátoru a prediktoru s nízkým řádem M
Zde se jedná vlastně o sériové řazení dvou filtrů nižších řádů, kdy estimátor se naladí, aby propouštěl jen parazitní složky rušení. S tím ale vybere i složky užitečného signálu blízko frekvence rušení, které ale chceme ponechat. Od toho je zde filtr prediktor, který už se nastavuje jen na složky signálu z estimátoru. Protože má omezený řád nevybere všechny, ale opět jako estimátor jen frekvence s nejvyšším podílem energie v signálu. Tedy se přesněji vyberou jen rušící frekvence a žádané další užitečné složky s menší energií se už nevyberou. Užitečné složky tedy zůstanou ve výstupním signálu. Na venek se bude struktura chovat jako jeden filtr o frekvenční charakteristice obrázek 4b. Z popisu je patrná jedna podmínka funkce. Aby s prediktor uplatnil, musí mít rušení větší energii než ostatní frekvenční složky žádaného signálu.
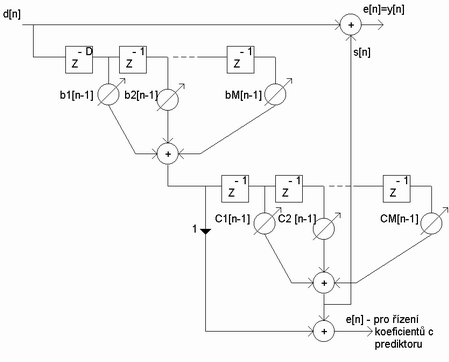
Obr. 2. Blokové schéma kaskádního zapojení adaptivních filtrů typu estimátor a prediktor
Koeficienty CP [n-1] filtru prediktoru jsou opět počítány metodou LMS stejným způsobem jako koeficienty bP [n-1] estimátoru. Pouze se pro ně používá jiný chybový signál e[n] - viz. obrázek 2.
Níže prezentované průběhy výsledky pak odpovídají pro řád filtrů estimátoru M1 = 25 a pro řád filtru prediktoru M2 = 25. Tedy při realizaci na DSP bude potřeba stejný počet paměťových míst jako pro jeden filtr estimátoru řádu M1= 50. Ale výsledný průběh charakteristiky bude dost odlišný viz. odstavec Příklad výsledku z testování struktur.
Příklad výsledku z testování struktur
Obě struktury jsem osobně testoval pomocí programu vytvořeného pro známý simulační program Matlab. Jako testovací vstupní signál jsem použil krátký zvukový signál se vzorkovací frekvencí 8kHz smíchaný se třemi sinusovými signály v čase proměnnou amplitudou o frekvencích f1 = 200Hz, f2 = 500 Hz a f3 = 1000 Hz - viz spektrum na obrázku 3. Na něm je vidět velká amplituda rušící složek. Zvukový signál je téměř nepatrný.
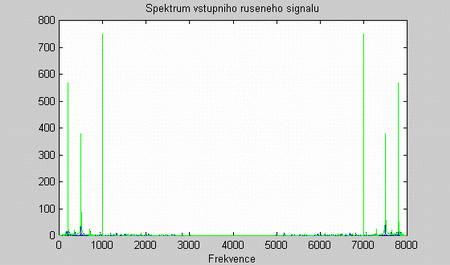
Obr. 3. Amplitudové spektrum vstupního signálu (zelený v jiném čase než modrý - proměnná amplituda).
Postupným testováním pro různé parametry mi, řády filtru M1 (M2) a D jsem nejlepších parametrů odfiltrování rušivých složek dosáhl pro hodnoty :
STRUKTURA 1 : M = 50 ( nebo M= 45 ) , D = 18 (nebo 22), mi= 0,0035 (mi = výkon signálu / 50)
STRUKTURA 2 : M1 = 25 a M2 = 25 ( nebo M1=30 a M2 = 30) , D = 18 (nebo 22), mi1= 0,0337 (mi1= výkon signálu / 10) a mi2 = 0,0337 (mi2= výkon signálu / 10)
Tomu odpovídají již frekvenční amplitudové charakteristiky na obrázku 3. již naučených filtrů na příslušné frekvence rušících sinusovek (tzn. s automaticky nastavenými koeficienty filtrů pomocí algoritmu LMS).
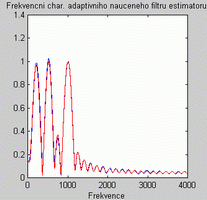
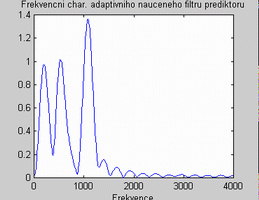
Obr. 4. Frekvenční amplitudové charakteristiky naučených adaptivních filtrů ( a) vlevo STRUKTURA 1 , b) vpravo STRUKTURA 2)
Jestliže porovnáme mimo řádů filtru ostatní parametry, významný rozdíl je vidět u hodnoty mi. Pro strukturu 2 jsou tyto hodnoty relativně vysoké, což znamená rychlé učení a rychlou reakci na změnu v signálu . U struktury 1 je hodnota nízká z důvodu omezování užitečného signálu. Při velké dynamice signálu se filtr estimátor rychle přelaïuje a díky vysokému řádu filtru potlačuje krátkodobé ale výrazné užitečné složky požadovaného signálu. Nízká hodnota konstanty mi tomuto jevu zamezuje.
Na posledním obrázku 5. jsou spektra obou výstupních signálů ze struktury 1 (vlevo) a struktury 2 (vpravo).
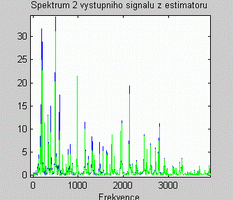
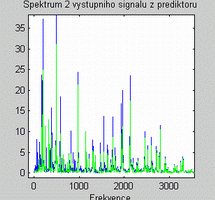
Obr. 5 . Amplitudová spektra výstupních signálů ( a) vlevo ze struktury 1, b) vpravo ze struktury 2 )
Porovnáním obou spekter je patrný lepší výsledek pro strukturu 1 adaptivního filtru typu estimátor. U toho se nejvíce shodují zelené spektrum ideálního čistého signálu a modrého signálu z výstupu filtru. Přestože se na frekvenční charakteristice estimátoru (obr. 4a) objevuje malé 3. pásmo, které vybírá a potlačuje frekvence okolo 700 Hz, má to menší vliv na výsledek než posunutá pásma filtru struktury 2, které přesně nevybírají rušící frekvence, ale frekvence "kousek vedle". To je způsobeno nízkým řádem filtrů struktury 2.
Závěr
V tomto článku jsem se pokusil přiblížit pojmy adaptivní filtrace a adaptivní filtr spolu s ukázkou výsledků z jednoduché simulace v programu Matlab na PC. Adaptivní FIR filtry s řídícím LMS algoritmem se často používají v různých modifikacích a samostatně nebo součástí větších a složitějších systému DSP (Digital Signal Processing). Lze je najít v systémech filtrace rušení, šumu, systémech hlasového ovládání a řízení, v nejmodernějších ústřednách pro VoIP (Voice Over IP) apod. Jejich jednoduchá struktura dovoluje jejich snadnou implementaci již na téměř všech CPU, MCU včetně malých mikrokotrolérů. Prostřednictvím jazyka C se implementace zjednodušuje na napsání 2 rovnic uvedených v tomto článku. Taková implementace na signálovém procesoru TI TMS320VC5416 ukázala srovnatelné výsledky s uvedenými.
Antonín Vojáček
vojacek@ hwg.cz
DOWNLOAD & Odkazy
- článek o FIR filtrech na stránkách automatizace.HW.cz - Použití filtrů FIR v digitálním zpracování signálů
- článek o bankách filtru na stránkách automatizace.HW.cz - Využití banky filtrů v digitálním zpracování signálů
- R. Vích, Z. Smékal: číslicové filtry. Academia 2000, http://www.cas.cz/ACADEMIA
- V. Davídek, M. Laipert, M. Vlček: Analogové a číslicové filtry. čVUT Praha 2000.