Tento článek pojednávající o úloze, principu a struktuře bank filtrů volně navazuje na článek "Použití filtrů FIR v digitálním zpracování signálů" uveřejněný na stránkách automatizace.HW.cz a v lednovém čísle tohoto roku 2005 v časopise Sdělovací technika.
Co to je Banka Filtrůť
Jak již asi název napovídá, jde o skupinu vzájemně propojených filtrů. To je pravda jen částečně, jak uvedu později. Úplně obecně je však možné to popsat následovně:
Banka filtrů je systém, kterým je možné libovolný digitální signál s frekvenčním rozsahem (pásmem) 0 Hz až fs/2 (polovina vzorkovací frekvence signálu) rozdělit do několika menších frekvenčních pásem (podpásmem), které pak lze odlišně zpracovávat. To znamená možnost různě zpracovávat různé frekvence signálu. Celý systém rozdělení signálu do podpásem však pracuje v časové oblasti, tzn. konkrétně s digitálními vzorky signálu, bez použití převodu do frekvenční oblasti například metodou Rychlé Fourierovy Transformace - FFT (Fast Fourier Transformation).
Toho pak se dá využít i ve zmíněné FFT, protože zatímco pro celý signál by musela být použita například 1024 vzorková FFT, v jednotlivých podpásmech banky filtrů stačí použít například 256 vzorkovou FFT v jednom pásmu a v jiném třeba jen 128 vzorkovou FFT dle potřeby. Tím se zjednodušší a zrychlý výpočet algoritmu v reálném čase, například na menších DSP procesorech či mikrokontrolérech, protože výpočetní náročnost banky filtrů v reálném čase je obvykle nižší než FFT. Ještě markantnější snížení počtu operací je při maticových výpočtech se vstupním signálem. Zatímco při práci s celým signálem by bylo nutné provádět maticové operace (násobení, sčítání apod.), po rozdělení signálu do podpásem je možné třeba použít jen implementačně jednoduché skalární operace.
K čemu to jeť
- Oddělené zpracování různých frekvencí signálu bez FFT
- Odstranění úzkopásmového šumu v signálu
- Snížení výpočetní náročnosti algoritmu jeho aplikací v podpásmech
- Různá intenzita a kvalita kódování různých frekvenčních složek signálu
- Odlišná velikost komprese pro různé frekvenční složky signálu
- Snížení bitového toku pro přenos
- Filtrace a zvýrazňování různých složek signálu
Banky filtrů se často využívá ve zpracování řeči (odšumování, detekce apod.), protože nejdůležitější složky řeči pro srozumitelnost se vyskytují v dolní polovině frekvenčního spektra a proto je vhodné detailněji zpracovávat tyto složky než vyšší frekvence, které nesou méně informace.
Druhy bank filtrů
Nejpoužívanější banky filtrů reprezentují dva typy, rozdělené podle principu dělení frekvenčního pásma:
- Lineární banka filtrů (viz. obrázek 1. a 2.) - frekvenční pásmo signálu je dělené na stejně velké podpásma.
- Oktávová banka filtrů (viz. obrázek 3. a 4.) - frekvenční pásmo je dělené oktávově na nestejně velká podpásma. Lépe vystihuje akustické vlastnosti sluchového ústrojí člověka.
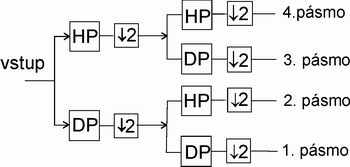
Obr. 1. Příklad rozkladu vstupního signálu lineární bankou filtrů
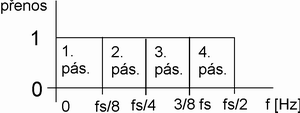
Obr. 2. Příklad rozdělení frekvenčního pásma signálu do podpásem 1 až 4 v lineární bance filtrů (obr. 1.)
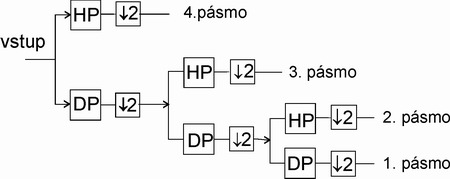
Obr. 3. Příklad rozkladu vstupního signálu oktávovou bankou filtrů s nestejnoměrným dělením
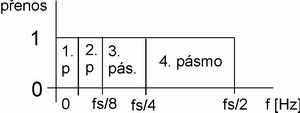
Obr. 4. Příklad rozdělení frekvenčního pásma signálu do podpásem 1 až 4 v oktávové bance filtrů (obr. 3.)
Princip a struktura banky filtrů
Celou banku filtrů lze rozdělit na analyzující a syntetizující část (viz. obrázek 5.). Analyzující část provádí rozklad vstupního signálu do definovaných pásem banky filtrů, naopak syntetizující část provádí zpětné složení částí signálu do jednoho na výstupu. Ten již obsahuje souhrn změn provedené na jednotlivé signály v podpásmech banky filtrů.
Banka filtrů je strukturálně složena z bloků:
- FIR filtry - vymezují frekvenční podpásma banky filtrů. Využívá se filtrů typu DP (Dolní Propust) a HP (Horní Propust) a všechny DP a HP filtry v jednotlivých stupních banky filtrů jsou stejné.
- Decimátor 2 - provádí snížení datového toku na polovinu a dvojnásobně sníží vzorkovací kmitočet signálu
- Interpolátor 2 - provádí zdvojnásobení datového toku a zdvojnásobí vzorkovací kmitočet signálu
Na obrázku 5. je příklad tzv. 4-kanálové lineární banky filtrů, tzn. rozděluje vstupní signál do 4 podpásem s rozsahem frekvencí 0 - fs/8,fs/8 - fs/4, fs/4 - 3fs/8, 3fs/8 - fs/2, kde fs je vzorkovací frekvence daného vstupujícího signálu.
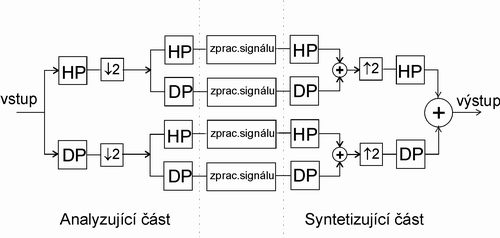
Obr. 5. Příklad kompletní 4-kanálové lineární banky filtrů s analyzující a systetizující částí
Souhrně decimaci, resp. interpolaci tvoří blok složený z FIR filtru a decimátoru, resp. interpolátoru, v pořadí, jak jsem je uvedl. FIR filtr zastává funkci zúžení spektra signálu. aby i po decimaci (interpolaci) byl splněn vzorkovací teorém, tzn. že v signálu se musí vyskytovat jen frekvence, pro které platí f < fs/2, kde fs je vzorkovací frekvence signálu. V opačném případě dochází ke známému aliasingu, kdy se nevratně a nerozdělitelně smíchají spektrální složky signálu. Při decimaci koeficientem D se sníží původní vzorkovací frekvence na hodnotu fsnew = fs/D. Proto je nutné použít FIR filtr s mezním kmitočtem propustného pásma fs/2D, kde fs je vzorkovací frekvence signálu před decimací, resp. po interpolaci.
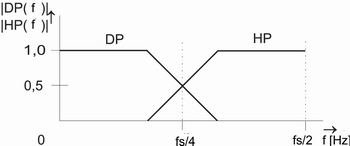
Obr. 6. Amplitudová asymptotická přenosová charakteristiky FIR filtrů pro banků filtrů (obr. 5.)
Pro případ banky filtrů se používá decimační koeficient 2 (viz. obrázek 5.), proto mezní kmitočet FIR filtru musí být fs/4. FIR filtry jsou klasické filtry s konečnou impulsovou odezvou (Finite Impulse Response) v řádu desítek s mezním kmitočtem propustného pásma fs/4 (obrázek 6.). Kvalitní banku filtrů dle obrázku 5. lze realizovat již s FIR řádu 21. Decimátor dvěma, je realizován vypouštěním každého druhého vzorku v datovém toku. Interpolátor dvěma je naopak realizován doplňováním nulového vzorku mezi každé dva vzorky datového toku.
Závěr
Banka filtrů je jednoduchá a implementačně nenáročná možnost, jak zpracovávat různá frekvenční pásma signálu různým způsobem v časové oblasti bez použití FFT (Fast Fourier Transformation). Zde uvedený článek je pouze informační a bližší informace můžete najít v publikacích uvedených v sekci DOWNLOAD & Odkazy nebo přímo mé osoby (viz. email níže).
Antonín Vojáček
vojacek@ hwg.cz
DOWNLOAD & Odkazy
- článek o FIR filtrech na stránkách automatizace.HW.cz- Použití filtrů FIR v digitálním zpracování signálů
- R. Vích, Z. Smékal: číslicové filtry. Academia 2000, http://www.cas.cz/ACADEMIA
- V. Davídek, M. Laipert, M. Vlček: Analogové a číslicové filtry. čVUT Praha 2000.
- J. Jan: číslicová filtrace, analýza a restaurace signálů. BEN 2004 - právě v prodeji.




