Jste zde

Vlnková transformace pro číslicové zprac. signálů

Antonín Vojáček, 14. Říjen 2006 - 9:22

Mnoho techniků zná nebo již slyšelo o Fourierově transformaci (FFT, STFT), pomocí které se získává průběh spektra analyzovaného signálu. Pokud však signál je v čase proměnný, výsledky již nejsou ideální. Pak tu je vlnková transformace, která umí přesně zobrazit parametry složek signálu v čase i frekvenci. Více se dozvíte v článku ...

Co je to vlnková transformace?

Vlnková transformace (Wavelet Transformation) je způsob, jak v libovolném signálu (např. zvuku, hudby, signálu ze senzoru) rozlišit jednotlivé komponenty, ze kterých je signál složen a ty vhodně zobrazit. Provádí tak něco podobného jako Fourierova transformace (FT) a její odvozené verze (DFT, FFT, STFT), avšak pro některé signály dosahuje daleko přesnějších výsledků. Vlnková transformace je tedy výpočetní algoritmus vhodný pro implementaci na DSP (signálovém procesoru) nebo v PC, založený na porovnávání analyzovaného signálu s předem vybraným krátkým vzorem průběhu, tzv. vlnkou. A právě hodnota/úroveň podobnosti pro různá posunutí a roztažení vlnky vůči signálu, je hledaným výsledkem transformace.

K čemu to je ?

Vlnková transformace (Wavelet Transformation) se dá využít k odfiltrování nežádoucích rušení nebo jako ztrátová komprese. Po rozložení signálu do komponent lze provést odstranění/vymazání složek s malým vlivem a opětovným složením tak získat digitální signál s menším počet dat, tj. velikostí souboru.

Odšumování a odrušování libovolných signálů - některé se však hodí více, jiné méně
Komprese signálů i v reálném čase - zvuku, hudby, obrazu, videa, signálů ze snímačů
Rozpoznávání hran a obrysů v obraze
Zvýrazňování určitých částí signálů

Na jakém principu vlnková transformace pracuje ?

Celý princip základní výpočetního algoritmu vlnkové (wavelet) transformace CWT (Continuous Wavelet Transformation) spočívá ve vzájemném porovnávání analogového signálu x(t) se zvoleným vzorovým tvarem, označovaným jako vlnka ψ (wavelet). Vzdáleně je to něco podobného, jako kdyby byly různě tvarované předměty porovnávány s nějakým základním geometrickým tvarem typu krychle, kvádr, válec, kužel nebo koule. Výsledkem porovnání je koeficient-hodnota CWT (τ, s) udávající úroveň podobnosti vzoru-vlnky se signálem.

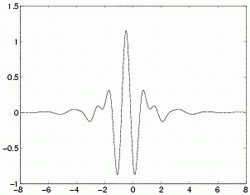
Obr. 1. Meyerova vlnka - průběh amplitudy vlnky (svislá osa) v čase t (vodorovná osa)

Protože analyzovaný signál je proti vzorové vlnce velmi dlouhý, je samotné porovnávání prováděné metodou postupného posouvání vlnky vůči signálu o konstantní krok = časové posunutí τ. Výsledkem je posloupnost-řada čísel udávající podobnost vlnky se signálem v konkrétním časovém okamžiku. Další věc je ta, že určitý kousek signálu může být vlnce tvarově podobný, pouze je proti ní časově prodloužený nebo smrsknutý. Například vlnka má délku 40 ms a kousek podobného průběhu signálu jen 20 ms. Proto se mimo časový posuv vlnky provádí i její postupné "roztahování" na různé délky, tzv. změna měřítka s.

CWT lze matematicky vyjádřit následujícím vztahem:

Celý postup výpočtu je tedy následující:

Vezme se analyzovaný signál x(t) a z "tabulkové nabídky" zvolený tvar vlnky ψ o určitém měřítku s. Postupným posouváním vlnky proti signálu se dle vzorce zjistí její podobnost v X konkrétních časových okamžicích. Poté provede změna měřítka vlnky a opětovné porovnání se signálem ve stejných časových okamžicích. A to se "provádí" pořád dokola, pro Y měřítek vlnky. Výsledkem je tedy matice hodnot podobností pro X čas. posunutí a Y měřítek vlnky. To je podobné jako u spektrogramu STFT (krátká Fourierova transformace - Short-Time Fourier Transformation), kde je výsledkem matice hodnot amplitud signálu pro X čas. posunutí a Y hodnot frekvencí. Porovnáním obou matic lze nalézt závislost mezi měřítkem vlnky s a frekvencí f, s=1/f. Tzn. že malá měřítka vlnky odpovídají zjištění vysokých frekvencí signálů.

Obr. 2. Porovnání spektrogramu vlnkové transformace (vlevo) a STFT (vpravo)

Velký rozdíl je ve výsledné "struktuře" matice. Zatímco v případě spektrogramu STFT je rozdělena na pravidelné, stejně velké oblasti, které nerespektují zkrácení časové periody signálu pro vysoké frekvence, "struktura" matice diskrétní vlnkové transformace DWT respektuje zkrácení časové periody vysokofrekvenčních složek analyzovaného signálu. Tzn. že algoritmus vlnkové transformace zahrnuje proměnnou délku okna, zatímco u STFT je délka okna stále fixní. Protože však obsah vyznačených obdélníků DWT je shodný s obsahem čtverců STFT, tzn. vyjadřují stejnou energie signálu, jsou si dosažené výsledky ekvivalentní.

Příklady některých nejpoužívanějších vlnek

Obr. 3. Vlnka Daubechies2 (vlevo) a Haarova vlnka (vpravo)

Obr.4. Vlnka Mexican hat (vlevo) a Morletova vlnka (vpravo, imaginární část čárkovaně)

Diskrétní Fourierova Transformace pomocí filtrace

DWT (Diskrétní Vlnková Transformace) lze chápat jako speciálně vzorkovanou CWT, kterou lze počítat rychlým algoritmem, tvořeným filtrací FIR filtry a podvzorkováním (decimací). Jeho nejpoužívanější verzí je ekvidistantní vzorkování v čase a logaritmické vzorkování v měřítku, které má umožňuje nestejnoměrně vzorkovat signál s ohledem na jeho časový nebo frekvenční průběh.

Obr. 5. Kvantizace/vzorkování CWT v prostoru čas-měřítko - vznik DWT

Nejpoužívanější praktická realizace DWT spočívá ve struktuře páru kvadraturních zrcadlových filtrů (QMF) tvořených dolní propustí DP (scaling filter) a horní propustí HP (wavelet filter), které mají komplementární propustná pásma. Základem dolní propusti je měřítková funkce a z ní vypočítaný měřítkový filtr w, z kterého normováním vzniknou koeficienty filtru dolní propusti h. Koeficienty horní propusti g pak vzniknou inverzí impulsní funkce dolní propusti h. Jednoduše lze tento návrh provést speciálními příkazy v programu Matlab doplněného o Wavelet Toolbox.

Obr. 6. Jedna vrstva filtrů DWT (vlevo) a rozklad na aproximace a detaily (vpravo)

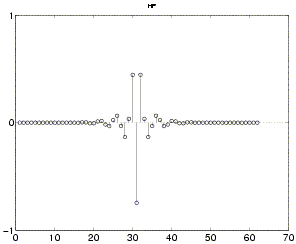
Obr. 7. Impusní odezva filtrů DP (vlevo) a HP (vpravo) pro Meyerovu vlnku

Výstupy obou filtrů jsou pak decimovány 2, tj. podvzorkovány na polovinu vstupních vzorků. Výsledkem filtrace každého stupně je posloupnost koeficientu/vzorků tzv. detailů DWT (cD) z větve s horní propustí HP a posloupnost koeficientů/vzorků tzv. aproximace (cA) z větve s dolní propust DP. Díky decimaci je celkový počet koeficientů po jednom kroku stejný jako počet vstupních vzorků. Koeficienty aproximace lze dále analyzovat dalším stupněm banky filtrů a obdržet tak další soubor koeficientů aproximace a detailů. Tak lze postupovat až do úplného vyčerpání informace ze vstupního signálu, to znamená, že již nelze žádná další detaily nalézt. Zajímavé je, že lze poslounost detailů z každého stupně lze zvlášť zpět převést do časové oblasti na signál stejné struktury jako na vstupu, pouze s tím rozdílem, že zde bude obsahovat jen příslušnou komponentu odpovídající daným detailům. Prakticky to lze přirovnat k rozložení vstupního analyzovaného signálu na jednotlivé frekvenční složky. Čím se použijí koeficienty větších detailů, tím se převodem získá více vysokofrekvenční složka.

Obr. 8. Analyzující/rozkládající část banky filtrů DWT transformace

Jednotlivé složky, které nechceme, aby signál obsahoval, nebo mají takový malý vliv (amplitudu), že jsou jen stěží rozpoznatelné, lze například úplně zahodit a jejich posloupnost nahradit nulama (nulovým signálem). Pak zpětnou transformací můžeme za pomoci syntetizující části banky filtrů opět spojit do jednoho signálu, která již však už nebude obsahovat vynulované složky. V syntetizující části banky filtrů se využívá rekonstrukčních FIR filtrů s koeficienty h' a g', které jsou určeny jako časově obrácené sekvence koeficientů dekompozičních filtrů h a g.

Obr. 9. Syntetizující/skládající část banky filtrů DWT transformace

K výpočtu lze však použít i jiné metody návrhu, například používající iterační postupy vycházejí z tzv. Daubechiesové dilatační rovnice.

Příklady výsledků z testování

Typickým příkladem, kdy DWT (Diskrétní vlnkové transformace) dosahuje výrazně lepších výsledků než Fourierova transformace, resp. SFTF (Short-Time Fourier Transformation), je analýza periodického signálu složeného ze třech sinusových složek, přičemž jedna má přerušovaný průběh.

Na obrázku 10. jsou uvedeny 3 průběhy spektrogramů pro harmonický signál složený ze dvou stálých sinusovek o frekvencích 10 a 13 Hz a jedné přerušované sinusovky o frekvenci 85 Hz. Na horním obrázku je spektrogram pro STFT s krátkým segmentovacím oknem. To sice umožňuje přesně lokalizovat místa zapnutí a vypnutí sinusovky 85 Hz, ale neumožňuje zjistit frekvence spodních dvou sinusovek. V prostředním spektrogramu je naopak zvoleno dlouhé segmentovací okno, které sice umožňuje přesně určit a lokalizovat frekvence, ale neumožňuje vůbec zjistit přerušení 3. sinusového signálu. Fourierova transformace se obecně vyznačuje vzájemnou neurčitostí určení frekvence a času.

Na nejspodnějším spektrogramu je výsledek vlnkové transformace, který díky jiné délce okna pro nízké a vysoké frekvence - viz obrázek 2. - umožňuje přesně lokalizovat jak průběh komponent signálu v časovém měřítku, tak i ve frekvenčním. A právě to je přínos Vlnkové (Wavelet) transformace.

Obr.10. Průběhy spektrogramů pro STFT (krátké okno - nahoře, dlouhé okno - uprostřed) a DWT (dole)

Závěr

Vlnková transformace se v posledních letech více a více rozšiřuje jako kvalitní metoda zpracování některých číslicových signálů. Není však vhodná pro všechny signály. Některé svým tvarem například nevyhovují ani jedné z mnoha nabízených vlnek. Obecně je pro stacionární signály a některé kvazistacionární signály typu řeč, vhodnější Fourierově transformace, zatímco pro zpracování hudby a obrazu zase se často jeví výhodnější právě vlnky. Vždy je však vhodné nejprve na "typickém" analyzovaném kousku signálu vyzkoušet obě metody a pak zvolit tu s vhodnějšími výsledky.

Poznámka: Článek jsem pojal jako stručný popis vlnkové transformace a zpracoval jsem ho spíše popisně. Čtenáře - odborníky na zpracování signálů a vývojáře, vyžadující přesný popis vzorci, odkazuji na níže uvedené stránky a dokumenty.

Antonín Vojáček
vojacek@ hwg.cz