FIR filtry jsou plně číslicové filtry pro zpracování libovolných digitálních signálů přímo v procesoru, který může provádět i další zpracování. Filtrace se provádí softwarově, tedy vykonáváním programu, bez jakékoliv externí součástkové podpory. Obecný popis struktury těchto filtrů, vlastností a použitelnosti v praxi popisuje následující článek.

Co jsou FIR filtry ť

Jde o plně číslicové filtry, které nemají ekvivalent v analogové oblasti zpracování signálů. Filtrují již plně digitální signál v podobě posloupnosti vzorků po převodu analogového signálu A/D převodníkem. FIR znamená Finite Impulse Response, tedy filtry s tzv. konečnou impulsovou odezvou (konečný počet nenulových výstupních hodnot po vybuzení filtru jednotkovým impulsem). K jejich praktické realizaci je potřeba nějaký procesor nebo dnes i vyspělá hradlová pole FPGA.

Vlastnosti FIR filtrů

Výhody :

• Jednoduchá struktura
• Jednoduchý návrh a testování již realizovaných filtrů ( koeficienty filtru = impulsová odezva )
• Vždy stabilní - dáno strukturou filtru (nehrozí rozkmitání)
• Malý vliv parazitních jevů reálné implementace - kvantování koeficientů, přetékání, limitní cykly
• často přímo podporované instrukcemi asembleru signálových procesorů (např. instr. FIRS u DSP Texas Instruments)

Nevýhody :

• Obvykle velký řád filtru -> velký počet koeficientů filtru (rozsáhlá struktura filtru)
• Výpočetní časová náročnost pro velké řády filtrů
• Omezené nastavení útlumu nepropustného pásma

K čemu slouží ť

Samotnou filtraci signálů v číslicové (digitální) oblasti se dá využít nejen pro úpravu frekvenčního spektra hudby, ale i pro snížení či eliminaci nežádoucího rušení obsažené například v signálech pro měření a regulaci nebo zvýšení přenosové rychlosti dat, resp. přechodné snížení datového toku s využitím decimace a interpolace bez ztráty informace (tzv. perfektní rekonstrukce). často FIR filtr zastávají úlohy ve složitějších systémech pro zpracování signálu, jakými jsou samočinné adaptivní filtry, banky filtrů nebo algoritmy pro snižení obsahu šumu (hluku) smíchaného například s řečí (například řeč a hluk v jedoucím automobilu).

Struktura filtrů FIR

FIR filtry patří mezi tzv. dopředné filtry, které obsahují jen dopředné vazby a tím jejich struktura netvoří integrátor (není zde zpětná vazba), jak je tomu u klasických IIR filtrů. Tím je zajištěna stabilita filtru proti rozkmitání a velká robustnost pro implementaci. Na následujícím obrázku 1. je blokově znázorněna struktura FIR filtru 3. řádu.

Obr. 1. Blokové schéma FIR filtru řádu 3

Bloky D (Delay) značí zpožïovací členy, což v praxi vyjadřuje paměťové místo v paměti procesoru a slouží k uložení právě předchozího vzorku. Více bloků D tvoří tzv. zpožïovací linku, tedy buffer. V uvedeném případě má délku třech paměťových míst a tedy jsou v něm uloženy vždy tři poslední (předchozí) vzorky signálu.Tyto tři vzorky jsou společně s novým vzorkem násobeny koeficienty filtru b0 až b3. Tyto koeficienty určují frekvenční přenosovou charakteristiku filtru. Na výstupu (v pravé části) blokového schéma se provádí sečtení všech mezivýsledků po násobení do výstupního vzorku, který pak reprezentuje přefiltrovaný signál. Na obrázku 2. je příklad porovnání ideální přenosové charakteristiky filtru a reálné charakteristiky filtru vzniklé zpětným převodem z koeficientů filtru.

Obr 2. Typický příklad frekvenční amplitudové charakteristiky (přenosové char.) FIR filtru

Návrh filtrů FIR

Přestože jsou FIR filtry jednoduché, není jejich návrh zcela triviální. Z praktického hlediska je nejjednodušší využít známého univerzálního maticového programu Matlab (téměř libovolné verze) firmy MathWork a použít funkce fir1.m a fir2.m v Signal processing toolboxu (nápověda syntaxe příkazu - help fir1 resp. help fir2). Díky tomu lze velmi jednoduše získat potřebné koeficienty filtru dle zadaných vlastností (řád filtru, mezní frekvence propustného pásma, zvolené okno), které pak už jen stačí vložit do struktury filtru v programu.

Při "ručním" návrhu filtru a výpočtu koeficientů se dá využít návrhu pomocí metody oken. Přesný popis a postup návrhu lze nalézt v následujících publikacích [1], [2], až [6] v rubrice Odkazy.

Cílem celého návrhu je tedy získat koeficienty b filtru. Volbou mezní frekvence propustného pásma se určuje kmitočet, na kterém má být pokles přenosu filtru -3dB. Volbou řádu filtru se určuje strmost přechodu přenosové frekvenční amlitudové charakteristiky mezi propustným a nepropustným pásmem a volbou tzv. okna se určuje minimální útlum filtru v nepropustné části charakteristiky. Zatímco u IIR filtrů lze poslední parametr téměř plynule měnit, u FIR filtrů jsme vázáni typem použitého okna, tedy jednou zvolenou hodnotou z následující tabulky 1.

Typ okna (nazev pro Matlab)	Útlum nepropustného pásma
obdelníkové (boxcar)	21 dB
trojúhelníkové (bartlett)	25 dB
Hannovo (hanning)	44 dB
Hammingovo (hamming)	53 dB
Blackmanovo (blackman)	74 dB

Tab. 1. Závislost útlumu nepropustného pásma FIR filtru na volbě okna při návrhu filtru

Prostředky k realizaci

Pro samotnou realizaci, tedy implementaci, filtrů FIR v praxi a v práci v reálném čase, je nutné použít vhodný procesor. Základní operace jsou dle obr.1. sčítání, násobení a posuv vzorků v datové paměti (realizace zpožïovací linky). Vhodné je tedy použít procesor s integrovanou hardwarovou násobičkou.

Nejvhodnější jsou tzv. signálové procesory (DSP - Digital Signal Processor), které již obsahují vše potřebné a často i přímo příkazy v asembleru pro jednoduchou implementaci FIR filtrů. Mezi nejznámější patří DSP Texas Instruments TMS320C32x, C50x, C54x, C64x a Motorola DSP56300. Na trhu se již objevují i kombinace klasického 8-bitového mikrokontroléru a DSP, jako je například dsPIC30xx od Microchips. V posledních letech se dají využít i vyspělé hradlové pole FPGA, které již mouhou mít integrovanou i násobičku (například FPGA Xillinx Spartan a Virtex).

Využití FIR filtrů v praxi

Jednoduchá filtrace rušení

Jak již bylo zmíněno v úvodu, FIR filtr se dá použít jako jednoduchý fiáltr rušení, jehož frekvenční složky se nemísí s užitečným signálem. Mějme například analogový senzor teploty, kde informace o teplotě v podobě nějaké elektrické veličiny se přenáší po nějakém kabelu k A/D převodníku a následnému zpracování. Na kabel působí rušení například harmonické rušení síťová frekvence 50Hz, které se pak převádní v A/D převodníku společně s užitečnou informací. To ukazuje blokové schéma na obrázku 2.

Obr. 3. Blokové schéma zpracování signálu ze senzoru

Jestliže nejrychlejší změna hodnoty měřené teploty je pomalejší (má nižší frekvenci) než perioda rušení, lze vhodným filtrem typu DP odfiltrovat rušení z užitečného signálu.

Obr. 4. Příklad filtrace rušení ve frekvenčním spektru pomocí FIR filtru

V praktické realizaci je nutné zvolit takovou vzorkovací frekvenci A/D převodníku, resp. kodeku, aby frekvenční spektrum přiváděného analogového signálu ještě tyto složky obsahovala. Podobně lze pásmovou propustí PP nebo horní propustí HP odfiltrovat rušení nižších frekvencí než je spektrum užitečného signálu.

Decimace / Interpolace signálu

Decimace je princip, kterým lze snížit počet snížit vzorků signálu (snížit datový tok) a ve spojení s interpolací na druhé straně přenosové cesty obnovit původní počet vzorku (datový tok) užitečného signálu aniž by došlo ke ztrátě informace (zkreslení užitečného digitálního signálu, tzv. perfektní rekonstrukce. To ale platí pouze za předpokladu, že frekvenční spektrum užitečného signálu je nižší než hodnota vzorkovací frekvence A/D převodníku dělená decimačním koeficientem (násobkem snížení počtu vzorků, resp. datového toku).

Složky signálu s vyšší frekvencí jsou nenávratně ztraceny. Blokové schéma takové přenosové cesty s decimací napočátku s decimací a na konci s interpolací, je na obrázku 5.

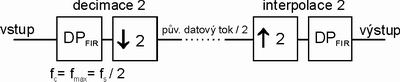
Obr. 5. Blokové schéma struktury pro snížení dat. toku (počtu vzorků) decimací / interpolací

Kritická frekvence fc filtrů FIR musí být navržena na udávaný kmitočet fsp/(2*D), kde fsp značí původní vzorkovací frekvenci vstupujícího signálu (před decimací), nebo fc=fs/2, kde fs=fsp/D. D zde značí decimační koeficient (na obrázku 5. D = 2, tedy fc=fsp/4). Decimace se může snadno realizovat vypuštěním (D - 1) vzorků z bloku D vzorků, tzn. pro D = 2 vypuštěním každého 2. vzorku. Interpolaci lze naopak vytvořit vkládáním nulových vzorků místo dříve vypuštěných.

Tohoto principu decimace / interpolace se využívá v tzv. bance filtrů. Ta umožňuje rozdělit celé frekvenční spektrum signálu do menších podpásem a každý tento užší úsek frekvencí rozdílně zpracovávat, například dle míry obsažené informace. Více o bankách filtrů lze se dozvědět v [4] nebo zadáním hesla filter bank do některého z internet vyhledávačů stránek.

Závěr

FIR filtry mohou být velmi dobrý prostředek pro filtraci libovolných digitálních signálů v reálném čase, jakými jsou hudba, řeč, datové signály z měření a senzorů apod. často se jim dává přednost v aplikacích, kde není potřeba velmi strmých přechodů propustného a nepropustného pásma a velký útlum v nepropustném pásmu. Skoro vždy se používají tam, kde je filtr součástí nějakého složitějšího systému (banka filtrů, adaptivní (samonastavující se) filtry), z důvodu jejich implementační robustnosti a zajištěné stabilitě.

Odkazy :

[1] R. Vích, Z. Smékal: číslicové filtry. Academia 2000, http://www.cas.cz/ACADEMIA - stále volně v prodeji
[2] Z. Smékal, R. Vích: Systémy zpracování signálů na signálových procesorech. Radix s.r.o. 1998. - stále volně v prodeji
[3] J. Jan: číslicová filtrace, analýza a restaurace signálů. BEN 2004 - právě v prodeji.
[4] V. Davídek, P. Sovka: číslicové zpracování signálů a implementace. Skripta čVUT Praha 2002.
[5] V. Davídek, M. Laipert, M. Vlček: Analogové a číslicové filtry. čVUT Praha 2000.
[6] J. Prchal, B. Šimák: Digitální zpracování signálů v telekomunikacích. Skripta čVUT Praha 2001.
[7] J. Jan : číslicová filtrace, analýza a restaurace. VUT Brno 1997.

Antonín Vojáček
vojacek @hwg.cz